(本题10分)在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B(8,0),斜边AO=10,C为AO的中点,反比例函数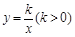 的图象经过点C,且与AB交于点D。
的图象经过点C,且与AB交于点D。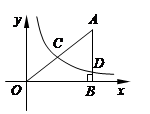
(1)求此反比例函数的解析式;
(2)求线段AD的长度。
相关知识点
推荐套卷
(本题10分)在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B(8,0),斜边AO=10,C为AO的中点,反比例函数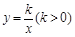 的图象经过点C,且与AB交于点D。
的图象经过点C,且与AB交于点D。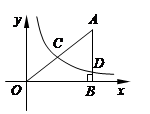
(1)求此反比例函数的解析式;
(2)求线段AD的长度。