甲、乙两个盒子里各放有标号为1，2，3，4的四个大小形状完全相同的小球，从甲盒中任取一小球，记下号码
后放入乙盒，再从乙盒中任取一小球，记下号码
.
（Ⅰ）求
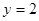的概率；
（Ⅱ）设随机变量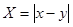
，求随机变量
的分布列及数学期望.
相关试题
，求证：
或
．
满足
，如果函数
在
时是增函数，则在
时，是增函数还是减函数？试证明．
的图象如图所示，求二次函数
的顶点的横坐标的取值范围．
，当
时有最小值8，求
的值．
lg[H
]，其中［H
摩尔／升，计算纯净水的pH．相关知识点
推荐套卷
甲、乙两个盒子里各放有标号为1，2，3，4的四个大小形状完全相同的小球，从甲盒中任取一小球，记下号码后放入乙盒，再从乙盒中任取一小球，记下号码.
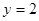（Ⅰ）求的概率；
（Ⅱ）设随机变量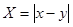，求随机变量的分布列及数学期望.
粤公网安备 44130202000953号