平面上有两个质点A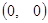
，B
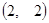，在某一时刻开始每隔1秒向上下左右任一方向移动一个单位. 已知质点A向左，右移动的概率都是
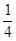，向上，下移动的概率分别是
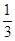和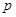
，质点B向四个方向移动的概率均为
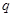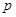.(1)求和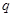的值；(2)试判断至少需要几秒，A、B能同时到达D
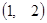，并求出在最短时间同时到达的概率？
相关试题
,n=
且m与n的夹角为
，
=4i-2j,
=7i+4j,
=3i+6j，求四边形ABCD的面积.
km的C,D两点
=75°,
=45°, 
=30°, 
=45°，
}中, 
,
,求
。
，
恒成立，求实数
的取值范围；
恒成立，求实数推荐套卷
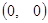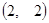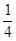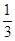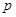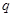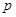平面上有两个质点A，B，在某一时刻开始每隔1秒向上下左右任一方向移动一个单位. 已知质点A向左，右移动的概率都是，向上，下移动的概率分别是和，质点B向四个方向移动的概率均为.(1)求和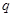的值；(2)试判断至少需要几秒，A、B能同时到达D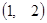，并求出在最短时间同时到达的概率？
粤公网安备 44130202000953号