某车间有10名工人,其中4人仅会车工,3人仅会钳工,另外3人车、钳工都会,现需选出6人完成一件,需要车工、钳工各3人,问有多少种选派方案?
分析:如果先考虑钳工,因有6人会钳工,故有C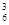 种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚其余的7人中有多少人会车工,因此在选车工时,就无法确定是从大局出7人中选,还是从6人、5人或4人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚其余的7人中有多少人会车工,因此在选车工时,就无法确定是从大局出7人中选,还是从6人、5人或4人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
(1)选出的6人中不含全能工人;
(2)选出的6人中含有一名全能工人;
(3)选出的6人中含有2名全能工人;
(4)选出的6人中含有31名全能工人;