设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: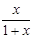
<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
，恒有不等式
是三个向量，试判断下列各命题的真假．
且
，则
在
的方向上的投影是一模等于
（
是
，
，其中
．
与
互相垂直；
与
的值(
为非零的常数)．
,
,当
为何值时，
与
垂直？
与
，满足
，求证：
相关知识点
推荐套卷
设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: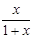<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
粤公网安备 44130202000953号