（本题12分）如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|=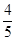
|PD|.
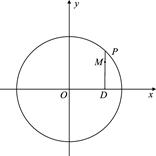
（Ⅰ）当P在圆上运动时，求点M的轨迹C的方程；
（Ⅱ）求过点（3,0）且斜率为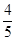的直线被曲线C所截线段的长度.
相关试题
满足
，
；(2)判断20是不是这个数列的项，并说明理由； (3)求这个数列前n项的和
。
>1的解集。
是公差不为零的等差数列，
，且
，
，
成等比数列.
，求数列
的前
项和.
的内角
、
的对边分别为
、
，
，
.
；
，求相关知识点
推荐套卷
（本题12分）如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的投影，M为PD上一点，且|M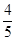D|=|PD|.
（Ⅰ）当P在圆上运动时，求点M的轨迹C的方程；
（Ⅱ）求过点（3,0）且斜率为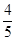的直线被曲线C所截线段的长度.
粤公网安备 44130202000953号