为了了解学生课业负担情况,某初中在本校随机抽取50名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,并将抽查结果绘制成了一个不完整的频数分布直方图(如图所示)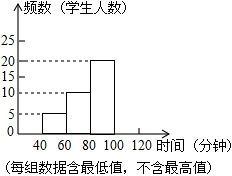
(1)请补全频数分布直方图;
(2)被抽查50名学生每天完成课外作业时间的中位数在_______组(填时间范围);
(3)若该校共有2400名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟).
相关知识点
推荐套卷
 与
与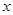 轴交于点A(
轴交于点A(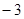 ,0),
,0), 轴的交点
轴的交点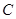 (0,3).
(0,3).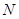 ,在抛物线上是否存在点
,在抛物线上是否存在点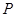 ,使得△NPC是以NC为直角边的直角三角形?若存在,求出点
,使得△NPC是以NC为直角边的直角三角形?若存在,求出点
 . 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?
. 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?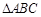 中,
中,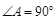 ,
,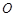 是
是 边上一点,以
边上一点,以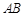 、
、 边相切于
边相切于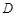 、
、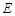 两点,连接
两点,连接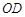 .已知
.已知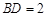 ,
, .求:
.求: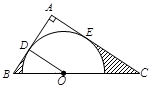
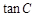 ;
;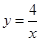 的图象上的概率;
的图象上的概率;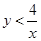 的概率.
的概率.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号