已知抛物线 与
与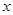 轴交于点A(
轴交于点A(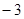 ,0),
,0),
(1)直接写出抛物线与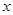 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)若直线过抛物线顶点M及抛物线与 轴的交点
轴的交点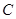 (0,3).
(0,3).
① 求直线MC所对应的函数关系式;
② 若直线MC与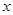 轴的交点为
轴的交点为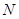 ,在抛物线上是否存在点
,在抛物线上是否存在点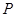 ,使得△NPC是以NC为直角边的直角三角形?若存在,求出点
,使得△NPC是以NC为直角边的直角三角形?若存在,求出点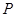 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 
相关知识点
推荐套卷
已知抛物线 与
与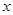 轴交于点A(
轴交于点A(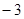 ,0),
,0),
(1)直接写出抛物线与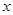 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)若直线过抛物线顶点M及抛物线与 轴的交点
轴的交点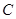 (0,3).
(0,3).
① 求直线MC所对应的函数关系式;
② 若直线MC与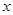 轴的交点为
轴的交点为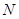 ,在抛物线上是否存在点
,在抛物线上是否存在点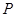 ,使得△NPC是以NC为直角边的直角三角形?若存在,求出点
,使得△NPC是以NC为直角边的直角三角形?若存在,求出点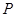 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 