已知 ,
,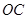 、
、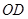 是过点
是过点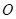 的射线,射线
的射线,射线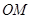 、
、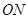 分别平分
分别平分 和
和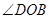 .
.
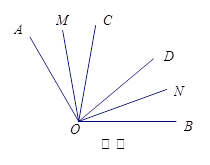
(1)如图①,若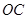 、
、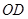 是
是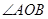 的三等分线,则
的三等分线,则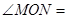 °
°
(2)如图②,若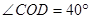 ,
,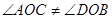 ,则
,则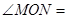 °
°
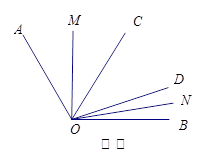
(3)如图③,在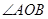 内,若
内,若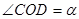 (
(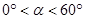 ),则
),则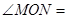 °
°

(4)将(3)中的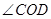 绕着点
绕着点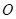 逆时针旋转到
逆时针旋转到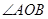 的外部(
的外部(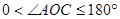 ,
,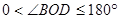 ),求此时
),求此时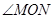 的度数.
的度数. 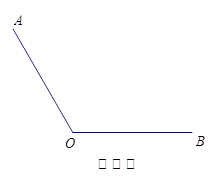
已知 ,
,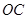 、
、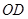 是过点
是过点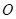 的射线,射线
的射线,射线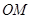 、
、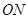 分别平分
分别平分 和
和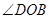 .
.
(1)如图①,若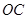 、
、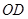 是
是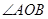 的三等分线,则
的三等分线,则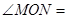 °
°

(2)如图②,若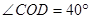 ,
,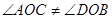 ,则
,则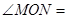 °
°

(3)如图③,在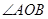 内,若
内,若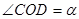 (
(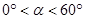 ),则
),则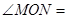 °
°

(4)将(3)中的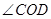 绕着点
绕着点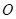 逆时针旋转到
逆时针旋转到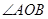 的外部(
的外部(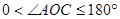 ,
,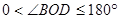 ),求此时
),求此时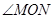 的度数.
的度数. 