正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
(1)填写下表:
| 正方形ABCD内点的个数 |
1 |
2 |
3 |
4 |
… |
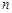 |
| 分割成的三角形的个数 |
4 |
6 |
|
|
… |
|
(2)原正方形能否被分割成2004个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由。
正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
(1)填写下表:
| 正方形ABCD内点的个数 |
1 |
2 |
3 |
4 |
… |
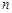 |
| 分割成的三角形的个数 |
4 |
6 |
|
|
… |
|
(2)原正方形能否被分割成2004个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由。