(本小题满分12分)
经市场调查,某旅游城市在过去的一个月内(以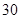 天计),第
天计),第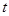 天
天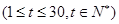 的旅游人数
的旅游人数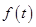 (万人)近似地满足
(万人)近似地满足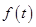 =4+
=4+ ,而人均消费
,而人均消费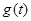 (元)近似地满足
(元)近似地满足 .
.
(Ⅰ)求该城市的旅游日收益 (万元)与时间
(万元)与时间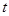
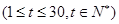 的函数关系式;
的函数关系式;
(Ⅱ)求该城市旅游日收益的最小值.
推荐套卷
(本小题满分12分)
经市场调查,某旅游城市在过去的一个月内(以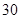 天计),第
天计),第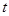 天
天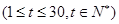 的旅游人数
的旅游人数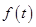 (万人)近似地满足
(万人)近似地满足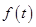 =4+
=4+ ,而人均消费
,而人均消费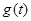 (元)近似地满足
(元)近似地满足 .
.
(Ⅰ)求该城市的旅游日收益 (万元)与时间
(万元)与时间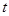
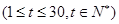 的函数关系式;
的函数关系式;
(Ⅱ)求该城市旅游日收益的最小值.