(本小题满分12分)
某建筑物的上半部分是多面体 , 下半部分是长方体
, 下半部分是长方体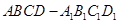 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.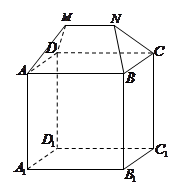

(Ⅰ)求直线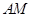 与平面
与平面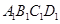 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)求该建筑物的体积.
推荐套卷
(本小题满分12分)
某建筑物的上半部分是多面体 , 下半部分是长方体
, 下半部分是长方体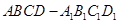 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.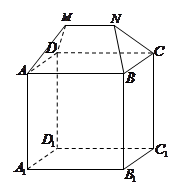

(Ⅰ)求直线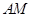 与平面
与平面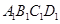 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)求该建筑物的体积.