(本小题14分)已知二次函数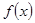 满足:
满足: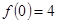 ,
,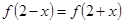 ,且该函数的最小值为1.
,且该函数的最小值为1.
⑴ 求此二次函数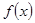 的解析式;
的解析式;
⑵ 若函数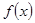 的定义域为
的定义域为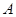 =
=  .(其中
.(其中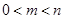 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数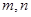 ,使得函数
,使得函数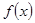 的值域也为
的值域也为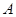 ?若存在,求出
?若存在,求出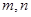 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
推荐套卷
(本小题14分)已知二次函数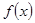 满足:
满足: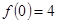 ,
,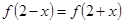 ,且该函数的最小值为1.
,且该函数的最小值为1.
⑴ 求此二次函数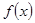 的解析式;
的解析式;
⑵ 若函数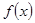 的定义域为
的定义域为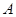 =
=  .(其中
.(其中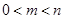 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数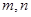 ,使得函数
,使得函数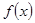 的值域也为
的值域也为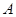 ?若存在,求出
?若存在,求出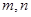 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.