学校举办“迎奥运”知识竞赛，设一、二、三等奖共12名，奖品发放方案如下表：
| 一等奖 |
二等奖 |
三等奖 |
| 1盒福娃和1枚徽章 |
1盒福娃 |
1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元，小明在购买“福娃”和微章前，了解到如下信息：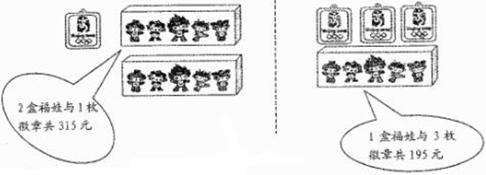
（1）求一盒“福娃”和一枚徽章各多少元？
（2）若本次活动设一等奖2名，则二等奖和三等奖应各设多少名？
相关试题
如图，在平面直角坐标系
中，一次函数
与反比例函数
的图象交于点
，与
轴交于点
，
轴于点
，
，
，
。
（1）求反比例函数和一次函数的解析式；
（2）若一次函数与反
比例函数的图象的另一交点为点
，连接
、
，求
，其中
满足
。为促进“平安重庆”建设，市公安局交巡警总队拟在我市某“三角形”转盘区域内新增一个交巡警平 台，使交巡警平台到三个十字路 a 的距离相等，试确定交巡警平台 P的位置．(要求：用尺规作图， 保留作图痕迹，不写已知、求作和作法)．
在同一直线上，
，
，且
。求证：
与
全等。
是格点三角形．在建立平面直角坐标系后，点
的坐标为（
）．
，画出
的坐标
；
按顺时针方向旋转
后得到
，画出
的坐标；
为位似中心放大，使放大前后对应边长的比为
，画出
的图形．
粤公网安备 44130202000953号