观察下列各式及其验算过程：
验证：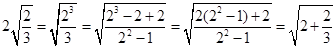
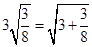
验证：
（1）按照上述两个等式及其验证过程的基本思路，猜想
的变形结果并进行验证；
（2）针对上述各式反映的规律，写出用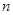
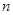（为任意自然数，且
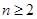）表示的等式，并证明
相关试题
．
．
相关知识点
推荐套卷
观察下列各式及其验算过程：
验证：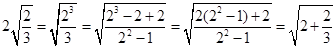
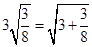
验证：
（1）按照上述两个等式及其验证过程的基本思路，猜想的变形结果并进行验证；
（2）针对上述各式反映的规律，写出用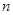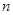（为任意自然数，且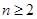）表示的等式，并证明
粤公网安备 44130202000953号