（本题8分）如图，已知点P是反比例函数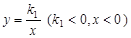
图像上一点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交反比例函数
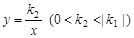图像于E、F两点．
（1）用含k1、k2的式子表示以下图形面积：
①四边形PAOB；② 三角形OFB；③四边形PEOF；
（2）若P点坐标为（－4，3），且PB︰BF＝2︰1，分别求出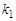
、
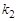的值．
化简，再求值，其中
，其中
，
．
，其中
，
．
，其中
．
，其中
，
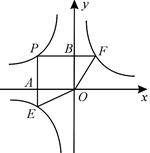
．相关知识点
推荐套卷
（本题8分）如图，已知点P是反比例函数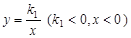图像上一点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交反比例函数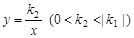图像于E、F两点．
（1）用含k1、k2的式子表示以下图形面积：
①四边形PAOB；② 三角形OFB；③四边形PEOF；
（2）若P点坐标为（－4，3），且PB︰BF＝2︰1，分别求出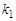、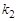的值．
粤公网安备 44130202000953号