统计表明,某种型号的汽车在匀速行驶中每小时的耗油量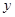 (升)关于行驶速度
(升)关于行驶速度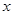 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
推荐套卷
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量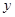 (升)关于行驶速度
(升)关于行驶速度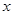 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?