某厂生产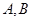
两型会议桌，每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套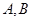型会议桌需要加工木材的时间分别为1小时和2小时，上油漆需要的时间分别为3小时和1小时。厂里规定：加工木材的时间每天不得超过8小时，上油漆的时间每天不得超过9小时。已知该厂生产一套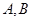型会议桌分别可获得利润2千元和3千元，试问：该厂每天应分别生产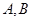两型会议桌多少套，才能获得最大利润？最大利润是多少？
相关试题
，用随机变量
表示A在1次实验中发生的次数。（1）求方差
的最大值；（2）求
的最大值。推荐套卷
某厂生产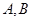两型会议桌，每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套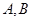型会议桌需要加工木材的时间分别为1小时和2小时，上油漆需要的时间分别为3小时和1小时。厂里规定：加工木材的时间每天不得超过8小时，上油漆的时间每天不得超过9小时。已知该厂生产一套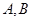型会议桌分别可获得利润2千元和3千元，试问：该厂每天应分别生产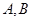两型会议桌多少套，才能获得最大利润？最大利润是多少？
粤公网安备 44130202000953号