已知:如图,在Rt△ABC中,∠ACB=90°,BC="3" ,tan∠BAC=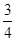 ,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系
,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系
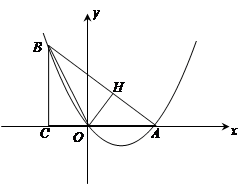
(1)求过A、B、O三点的抛物线解析式;
(2)若在线段AB上有一动点P,过P点作x轴的垂线,交抛物线于M,设PM的长度等于d,试探究d有无最大值,如果有,请求出最大值,如果没有,请说明理由.
(3)若在抛物线上有一点E,在对称轴上有一点F,且以O、A、E、F为顶点的四边形为平行四边形,试求出点E的坐标.