(11·湖州)(本小题10分)
我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表:
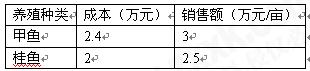
⑴2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共 收益多少万元?(收益=销售额-成本)
收益多少万元?(收益=销售额-成本)
⑵2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
⑶已知甲鱼每亩需要饲料500㎏,桂鱼每亩需要饲料700㎏,根据⑵中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少㎏?