(本小题13分) 已知数列{a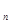
}满足0<a
, 且
(n
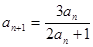N*).
(1) 求证：an＋1≠an；
(2) 令a1＝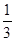
，求出a2、a3、a4、a5的值，归纳出an , 并用数学归纳法证明.
，1＋
为空间四边形
的边
上的点，且
，求证：
.
中
，
面
，
，
面
.
、
满足：
.
；
为等差数列，并求数列
，求实数
为何值时
恒成立。相关知识点
推荐套卷
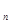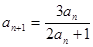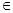(本小题13分) 已知数列{a}满足0<a, 且 (nN*).
(1) 求证：an＋1≠an；
(2) 令a1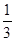＝，求出a2、a3、a4、a5的值，归纳出an , 并用数学归纳法证明.
粤公网安备 44130202000953号