将52名志愿者分成A,B两组参加义务植树活动，A组种植150捆白杨树苗，B组种植200捆沙棘树苗. 假定A,B两组同时开始植树.
（1）根据历年统计，每名志愿者种植一捆白杨树苗用时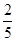
小时，种植一捆沙棘用时
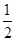小时，应如何分配A,B两组的人数，使植树活动持续的时间最短？
（2）在按（1）分配的人数种植1小时后发现，每名志愿者种植一捆白杨仍用时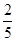小时，而每名志愿者种植一捆沙棘实际用时
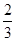小时，于是，从A组抽调6名志愿者加入B组继续种植，求植树活动持续的时间.
中，内角
的对边长分别为
。已知
，且
，求
。
中，
，求
项和
。
。
.
时，
恒成立？若存在，求a的取值范围，若不存在，说明理由.
与直线
相交于A、B两点，且OA丄OB(O为坐标原点).
的交点坐标：
时，求椭圆E的方程.推荐套卷
将52名志愿者分成A,B两组参加义务植树活动，A组种植150捆白杨树苗，B组种植200捆沙棘树苗. 假定A,B两组同时开始植树.
（1）根据历年统计，每名志愿者种植一捆白杨树苗用时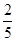小时，种植一捆沙棘用时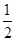小时，应如何分配A,B两组的人数，使植树活动持续的时间最短？
（2）在按（1）分配的人数种植1小时后发现，每名志愿者种植一捆白杨仍用时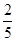小时，而每名志愿者种植一捆沙棘实际用时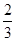小时，于是，从A组抽调6名志愿者加入B组继续种植，求植树活动持续的时间.
粤公网安备 44130202000953号