已知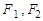
为双曲线
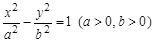的左、右焦点．
（Ⅰ）若点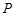
为双曲线与圆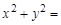
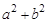的一个交点，且满足
，求此双曲线的离心率；
（Ⅱ）设双曲线的渐近线方程为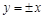
，
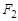到渐近线的距离是
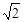，过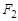的直线交双曲线于A，B两点，且以AB为直径的圆与
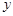轴相切，求线段AB的长．
．
；
，
，
中至少有一个不小于
．
的最大值．
，
，求证：
．
的点
上？
的一条焦点弦AB被焦点F分成长为m、n的两部分，求证：
为定值推荐套卷
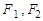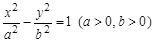已知为双曲线的左、右焦点．
（Ⅰ）若点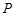为双曲线与圆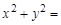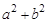的一个交点，且满足，求此双曲线的离心率；
（Ⅱ）设双曲线的渐近线方程为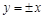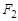，到渐近线的距离是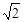，过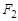的直线交双曲线于A，B两点，且以AB为直径的圆与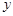轴相切，求线段AB的长．
粤公网安备 44130202000953号