已知双曲线的中心在原点，焦点
在坐标轴上，离心率为
，且过点（4，-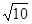
）（1）求双曲线的方程.（2）若点M(3,m)在双曲线上，求证：
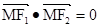.（3）若点A,B在双曲线上，点N(3,1)恰好是AB的中点，求直线AB的方程(12分)
相关试题
中，
，前10项和
；（1）求通项；（2）若从数列
项、……按原来的顺序组成一个新的数列
，求数列
项和
；
的前项和为
，且
，
为等差数列，且
，
．
，求数列
的前
项和
．
，且
，求
的最大值．
，
，
边上的高为
，求角
的大小与边
的长
，
）对称.推荐套卷
已知双曲线的中心在原点，焦点在坐标轴上，离心率为，且过点（4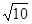，-）（1）求双曲线的方程.（2）若点M(3,m)在双曲线上，求证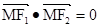：.（3）若点A,B在双曲线上，点N(3,1)恰好是AB的中点，求直线AB的方程(12分)
粤公网安备 44130202000953号