以下是在某地的旧房屋的销售价格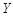
和房屋的面积x的数据：
房屋面积（ ） |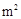
115 |
110 |
80 |
135 |
105 |
| 销售价格（万元） |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中画出回归直线；
（3）据（2）的结果估计当房屋面积为150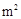时的销售价格．
与圆
相交于点
和点
。
与
的交点，且平行于直
的直线方程。
是实数,且
. 
求证:u为纯虚数; 
的最小值.
）=4-3i，求复数z.推荐套卷
以下是在某地的旧房屋的销售价格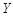和房屋的面积x的数据：
| 房屋面积（） |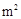
115 |
110 |
80 |
135 |
105 |
| 销售价格（万元） |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中画出回归直线；
（3）据（2）的结果估计当房屋面积为150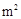时的销售价格．
粤公网安备 44130202000953号