为了解南宁市的绿化进程,小红同学查询了首府园林绿化政务网,根据网站发布的近几年南宁市城市绿化资源情况的相关数据,绘制了如下统计图(不完整):
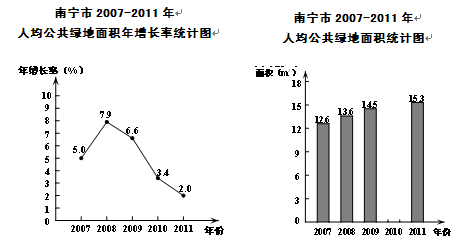
(1)请根据以上信息解答下列问题:
① 2010年南宁市人均公共绿地面积是多少平方米?(精确到0.1)
② 补全条形统计图;
(2)为提高南宁市人均公共绿地面积做贡献. 小红所在学校参加了南宁市植树造林活动,她对所在班级的40名同学2012年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
种树棵数(棵)
|
0
|
1
|
2
|
3
|
4
|
5
|
人数
|
2
|
1
|
3
|
12
|
13
|
9
|
如果按照小红的统计数据,请你通过计算估计,她所在学校的1500名同学在2012年共植树多少棵.