某商场为经营一批每件进价是10元的小商品,对该商品进行为期5天的市场试销.下表是市场试销中获得的数据.
销售单价/元
|
65
|
50
|
45
|
35
|
15
|
日销售量/件
|
15
|
60
|
75
|
105
|
165
|
根据表中的数据回答下列问题:
(1)试销期间,这个商场试销该商品的平均日销售利润是多少?
(2)试建立一个恰当的函数模型,使它能较好地反映日销售量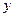 (件)与销售单价
(件)与销售单价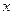 (元)之间的函数关系,并写出这个函数模型的解析式;
(元)之间的函数关系,并写出这个函数模型的解析式;
(3)如果在今后的销售中,该商品的日销售量与销售单价仍然满足(2)中的函数关系,试确定该商品的销售单价,使得商场销售该商品能获得最大日销售利润,并求出这个最大的日销售利润.