(本小题满分12分)经市场调查，某种商品在过去50天的销售量和价格均为销售时间t（天）的函数，已知前30天价格为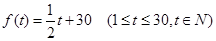
，后20天价格为f（t）="45" （31£ t £50, tÎN）,且销售量近似地满足g（t）=" -2t+200" （1£t£50, tÎN）．
（I）写出该种商品的日销售额S与时间t的函数关系式；
（II）求日销售额S的最大值．
的定义域为
，对定义域内
、
，都有
=
, 且当
时, 
.
、
的值；（2）求证：
上是增函数.
在
上的最小值.
函数
的定义域为集合
,
(2)
(3) (
(2) 求函数
的定义域和值域.推荐套卷
(本小题满分12分)经市场调查，某种商品在过去50天的销售量和价格均为销售时间t（天）的函数，已知前30天价格为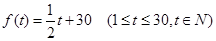，后20天价格为f（t）="45" （31£ t £50, tÎN）,且销售量近似地满足g（t）=" -2t+200" （1£t£50, tÎN）．
（I）写出该种商品的日销售额S与时间t的函数关系式；
（II）求日销售额S的最大值．
粤公网安备 44130202000953号