(本小题满分12分)已知函数 ,
, ,
,
(1) 判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2) 判断 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
(3) 若 ,方程
,方程 是否有根?如果有根
是否有根?如果有根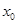 ,请求出一个长度为1的区间
,请求出一个长度为1的区间 ,使
,使 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间 的长度=
的长度= )
)
推荐套卷
(本小题满分12分)已知函数 ,
, ,
,
(1) 判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2) 判断 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
(3) 若 ,方程
,方程 是否有根?如果有根
是否有根?如果有根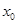 ,请求出一个长度为1的区间
,请求出一个长度为1的区间 ,使
,使 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间 的长度=
的长度= )
)