在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f,
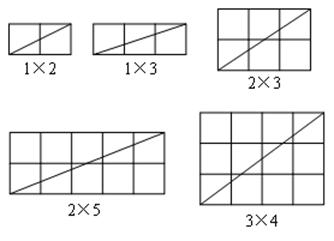
(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:
m
|
n
|
m+n
|
f
|
1
|
2
|
3
|
2
|
1
|
3
|
4
|
3
|
2
|
3
|
5
|
4
|
2
|
5
|
6
|
|
3
|
5
|
7
|
|
猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n的关系式是______________________________(不需要证明);
(2)当m、n不互质时,请画图验证你猜想的关系式是否依然成立,