某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出制作纪念册的册数 与甲公司的收费
与甲公司的收费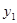 (元)的函数关系式.
(元)的函数关系式.
(2)请写出制作纪念册的册数 与甲公司的收费
与甲公司的收费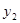 (元)的函数关系式.
(元)的函数关系式.
(3)如果学校派你去甲、乙两甲公司订做纪念册,你会选择哪家公司?
某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出制作纪念册的册数 与甲公司的收费
与甲公司的收费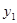 (元)的函数关系式.
(元)的函数关系式.
(2)请写出制作纪念册的册数 与甲公司的收费
与甲公司的收费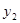 (元)的函数关系式.
(元)的函数关系式.
(3)如果学校派你去甲、乙两甲公司订做纪念册,你会选择哪家公司?