(本小题12分)某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入 万元,每件产品的成本将降低
万元,每件产品的成本将降低 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少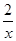 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(Ⅰ)求 的函数解析式;
的函数解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时 的值.
的值.
推荐套卷
(本小题12分)某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入 万元,每件产品的成本将降低
万元,每件产品的成本将降低 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少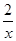 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(Ⅰ)求 的函数解析式;
的函数解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时 的值.
的值.