如图，△ABC中，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．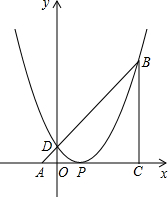
（1）用m的代数式表示点A、D的坐标；
（2）求这个二次函数关系式；
（3）点Q（x，y）为二次函数图象上点P至点B之间的一点，连接PQ、BQ，当x为何值时，四边形ABQP的面积最大？
相关试题
的面积． 
关于
轴的对称图形
．
的坐标．
+
—
（2）求x的值：
的对称轴是
，并且经过（－2，－5）和（5，－12）两点．相关知识点
推荐套卷
如图，△ABC中，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．
（1）用m的代数式表示点A、D的坐标；
（2）求这个二次函数关系式；
（3）点Q（x，y）为二次函数图象上点P至点B之间的一点，连接PQ、BQ，当x为何值时，四边形ABQP的面积最大？
粤公网安备 44130202000953号