如图：正方体ABCD-A1B1C1D1，过线段BD1上一点P（P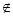
平面ACB1）作垂直于D1B的平面分别交过D1的三条棱于E、F、G．
(1)求证：平面EFG∥平面A CB1，并判断三角形类型；
(2)若正方体棱长为a，求△EFG的最大面积，并求此时EF与B1C的距离．
为两个互相垂直的单位向量，求
是两个垂直的单位向量，且
（２）若
的值。
满足
求
夹角为
， 
的值。
推荐套卷
如图：正方体ABCD-A1B1C1D1，过线段BD1上一点P（P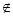平面ACB1）作垂直于D1B的平面分别交过D1的三条棱于E、F、G．
(1)求证：平面EFG∥平面A CB1，并判断三角形类型；
(2)若正方体棱长为a，求△EFG的最大面积，并求此时EF与B1C的距离．
粤公网安备 44130202000953号