作图：
（1）在图1中画出△ABC关于点O的中心对称图形。
（2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图2正方形网格（每个小正方形边长为1）中画出格点△DEF，使DE=DF=5，EF=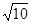
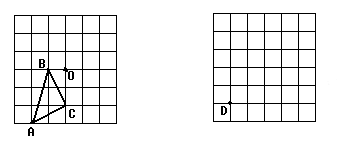
(图1) （图2）
相关试题
，判断直线BC与ED的位置关系并请说明理由.
.
，求出∠BOD的的度数；
（2）
，其中
.相关知识点
推荐套卷
作图：
（1）在图1中画出△ABC关于点O的中心对称图形。
（2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图2正方形网格（每个小正方形边长为1）中画出格点△DEF，使DE=DF=5，EF=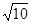
(图1) （图2）
粤公网安备 44130202000953号