2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段
|
频数
|
频率
|
50.5~60.5
|
16
|
0.08
|
60.5~70.5
|
40
|
0.2
|
70.5~80.5
|
50
|
0.25
|
80.5~90.5
|
m
|
0.5
|
90.5~100.5
|
24
|
n
|
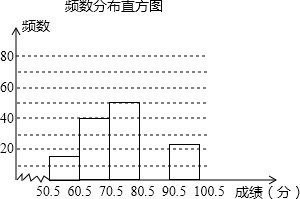
(1)这次抽取了名学生的竞赛成绩进行统计,其中:m=,n;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?