已知二次函数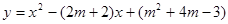 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
(1)求这个二次函数的解析式;
(2)点C是抛物线与 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
(3)在(2)的情况下,求四边形ACQD的面积.
相关知识点
推荐套卷
已知二次函数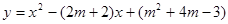 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
(1)求这个二次函数的解析式;
(2)点C是抛物线与 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
(3)在(2)的情况下,求四边形ACQD的面积.