某校从高一年级期末考试的学生中抽出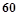
名学生，其成绩（均为整数）的频率分布直方图如图所示：
（Ⅰ）估计这次考试的及格率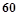（分及以上为及格）和平均分；
（Ⅱ）从成绩是
分以上（包括分）的学生中选两人，求他们在同一分数段的概率.
，AC=3，sinC="2sinA"
的值
（其中
）的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个最低点为
．
的解析式；
，求
中，
所对的边分别为
，
，
．
；
，求
，已知
，求角A，B，C的大小。
的长度的最大值；
，且
，求
的值。推荐套卷
某校从高一年级期末考试的学生中抽出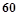名学生，其成绩（均为整数）的频率分布直方图如图所示：
（Ⅰ）估计这次考试的及格率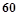（分及以上为及格）和平均分；
（Ⅱ）从成绩是分以上（包括分）的学生中选两人，求他们在同一分数段的概率.
粤公网安备 44130202000953号