如图,已知矩形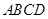 的边长
的边长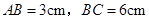 .某一时刻,动点
.某一时刻,动点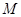 从
从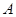 点出发沿
点出发沿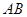 方向以
方向以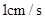 的速度向
的速度向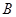 点匀速运动;同时,动点
点匀速运动;同时,动点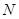 从
从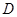 点出发沿
点出发沿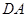 方向以
方向以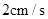 的速度向
的速度向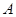 点匀速运动,设运动时间为t秒,问:
点匀速运动,设运动时间为t秒,问:
(1)用含t的代数式表示AN=___________cm;
(2)当t为何值时,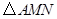 的面积等于矩形
的面积等于矩形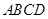 面积的
面积的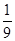 ?
?
(2)是否存在时刻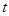 ,使以
,使以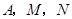 为顶点的三角形与
为顶点的三角形与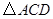 相似?若存在,求
相似?若存在,求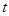 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.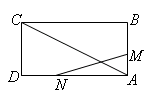
推荐套卷
如图,已知矩形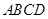 的边长
的边长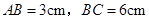 .某一时刻,动点
.某一时刻,动点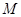 从
从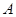 点出发沿
点出发沿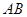 方向以
方向以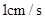 的速度向
的速度向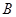 点匀速运动;同时,动点
点匀速运动;同时,动点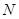 从
从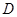 点出发沿
点出发沿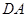 方向以
方向以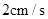 的速度向
的速度向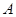 点匀速运动,设运动时间为t秒,问:
点匀速运动,设运动时间为t秒,问:
(1)用含t的代数式表示AN=___________cm;
(2)当t为何值时,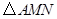 的面积等于矩形
的面积等于矩形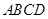 面积的
面积的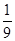 ?
?
(2)是否存在时刻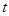 ,使以
,使以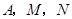 为顶点的三角形与
为顶点的三角形与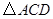 相似?若存在,求
相似?若存在,求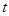 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.