射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):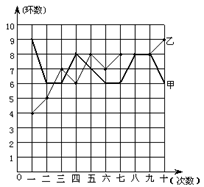
⑴根据图中所提供的信息填写下表:
⑵如果你是教练,会选择哪位运动员参加比赛?请结合上表中三个统计指标以及折线统计图说明理由。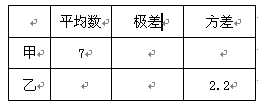
相关知识点
推荐套卷
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):
⑴根据图中所提供的信息填写下表:
⑵如果你是教练,会选择哪位运动员参加比赛?请结合上表中三个统计指标以及折线统计图说明理由。