如图,数轴上的点A、B、O、C、D分别表示-5、-1.5、0、2.5、6,回答下列问题.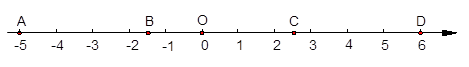
(1)O、C以及B、D两点间的距离各是多少?
(2)你能发现所得的距离与这两点所对应的数的差有什么关系吗?并请说出这个关系;
(3)假如数轴上任意两点A、B所表示的数是a、b,请你用一个式子表示这两点间的距离.
如图,数轴上的点A、B、O、C、D分别表示-5、-1.5、0、2.5、6,回答下列问题.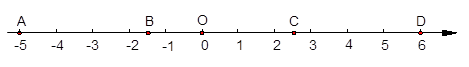
(1)O、C以及B、D两点间的距离各是多少?
(2)你能发现所得的距离与这两点所对应的数的差有什么关系吗?并请说出这个关系;
(3)假如数轴上任意两点A、B所表示的数是a、b,请你用一个式子表示这两点间的距离.