已知圆C的圆心在直线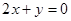
上，并经过A
，
两点。
(1)求圆C的方程。
(2)若直线l与圆C相切，且在x轴和y轴上的截距相等，求直线l的方程；
(3)已知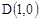
，从圆C外一点P(x，y)向圆引一条切线，切点为M. 且有|PM|＝|PD|，求使得|PM|取得最小值的点P的坐标.
相关试题
在区间[0,2]上的最小值为3，求a的值．
中，三条边
所对的角分别为
，向量
，
且满足
。
的大小；
成等比数列，且
，求
的值。
CD中，
.
,求m的值。推荐套卷
已知圆C的圆心在直线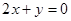上，并经过A，两点。
(1)求圆C的方程。
(2)若直线l与圆C相切，且在x轴和y轴上的截距相等，求直线l的方程；
(3)已知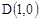，从圆C外一点P(x，y)向圆引一条切线，切点为M. 且有|PM|＝|PD|，求使得|PM|取得最小值的点P的坐标.
粤公网安备 44130202000953号