已知
、
两个盒子中分别装有标记为
，
，
，
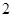的大小相同的四个小球，甲从盒中等可能地取出个球，乙从盒中等可能地取出个球．
（1）用有序数对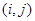
表示事件“甲抽到标号为i的小球，乙抽到标号为是j的小球”，求取出的两球标号之和为5的概率；
（2）甲、乙两人玩游戏，约定规则：若甲抽到的小球的标号比乙大，则甲胜；反之，则乙胜．你认为此规则是否公平？请说明理由．
相关试题
曲线
最高点到相邻的最低点间曲线与x轴交于一点(6,0),求函数解析式,并求函数在
上的值域.
=2,sin
)，
-α)-sin(
的值;
中，
.
项和记为
，证明：
。
中，底面
是正方形，侧棱
=2，
，垂足为F。推荐套卷
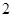已知、两个盒子中分别装有标记为，，，的大小相同的四个小球，甲从盒中等可能地取出个球，乙从盒中等可能地取出个球．
（1）用有序数对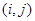表示事件“甲抽到标号为i的小球，乙抽到标号为是j的小球”，求取出的两球标号之和为5的概率；
（2）甲、乙两人玩游戏，约定规则：若甲抽到的小球的标号比乙大，则甲胜；反之，则乙胜．你认为此规则是否公平？请说明理由．
粤公网安备 44130202000953号