甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
| 甲 |
8 |
6 |
7 |
8 |
6 |
5 |
9 |
10 |
4 |
7 |
| 乙 |
6 |
7 |
7 |
8 |
6 |
7 |
8 |
7 |
9 |
5 |
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差;
公式:
(3)根据计算结果,估计一下两人的射击情况.
推荐套卷
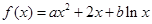 在
在 和
和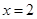 处取得极值,
处取得极值,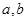 的值;
的值;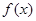 在
在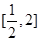 上的最大值和最小值.
上的最大值和最小值.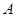 饮料,另外4杯为
饮料,另外4杯为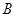 饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯
饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯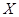 表示此人选对
表示此人选对 的展开式中,第4项和第9项的二项式系数相等,
的展开式中,第4项和第9项的二项式系数相等,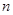 ,
,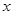 的一次项的系数.
的一次项的系数.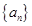 中,
中,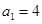 ,
, ,(1)求证:数列
,(1)求证:数列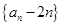 为等比数列。(2)设数列
为等比数列。(2)设数列 项和为
项和为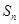 ,若
,若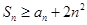 ,求正整数列
,求正整数列 粤公网安备 44130202000953号
粤公网安备 44130202000953号