某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为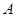 饮料,另外4杯为
饮料,另外4杯为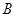 饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯
饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯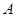 饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令
饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令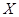 表示此人选对
表示此人选对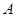 饮料的杯数.假设此人对
饮料的杯数.假设此人对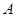 和
和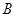 两种饮料没有鉴别能力.
两种饮料没有鉴别能力.
(1)求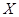 的分布列;
的分布列;
(2)求此员工月工资被定为2100元的概率.
相关知识点
推荐套卷
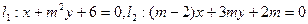 ,当
,当 为何值时,
为何值时,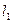 与
与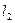 (1)相交;(2)平行;(3)重合?
(1)相交;(2)平行;(3)重合?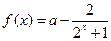 是奇函数
是奇函数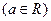 .
.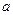 的值;
的值; 在(
在(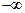 ,
,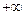 )上的单调性,并
)上的单调性,并 证明你的结论;
证明你的结论;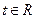 ,不
,不 等式
等式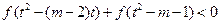 恒成立,求实数
恒成立,求实数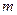 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
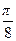 )的值;
)的值;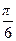 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.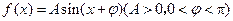 ,
,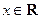 的最大值是1,其图像经过点
的最大值是1,其图像经过点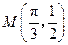 .
.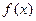 的解析式;
的解析式;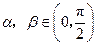 ,且
,且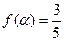 ,
,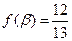 ,求
,求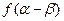 的值.
的值.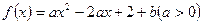 在区间
在区间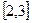 上的值域为
上的值域为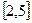
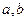
 的值
的值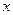 的函数
的函数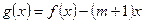 在
在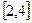 上为单调函数,求
上为单调函数,求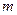 的取值范围
的取值范围 粤公网安备 44130202000953号
粤公网安备 44130202000953号