（本小题满分13分）如图（甲），在直角梯形ABED中，AB//DE，AB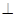
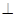BE，ABCD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点，现将△ACD沿CD折起，使平面ACD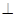平面CBED,如图（乙）．
（1）求证：平面FHG//平面ABE；
（2）记
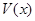表示三棱锥B－ACE 的体积，求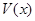的最大值；
（3）当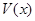取得最大值时，求二面角D－AB－C的余弦值．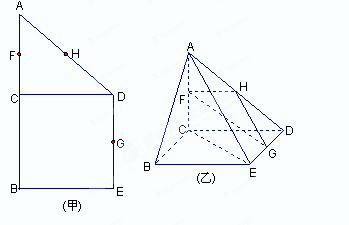
相关试题
和矩形
所在平面互相垂
,
为
的中点,
。
；
的大小。
。
的最小正周期;
个单位后，在
是增函数，当
最小时，求
（
∈N+）的图像关于y轴对称，且在（0，+∞）上是减函数，求满足
的实数
取值范围.
=
，（
∈ R）是R上的奇函数.
>
.
=
的值域是R，且在（-∞,1-
）上是减函数，求实数
的取值范围.推荐套卷
（本小题满分13分）如图（甲），在直角梯形ABED中，AB//DE，ABBE，AB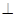CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点，现将△ACD沿CD折起，使平面ACD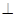平面CBED,如图（乙）．
（1）求证：平面FHG//平面ABE；
（2）记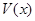表示三棱锥B－ACE 的体积，求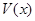的最大值；
（3）当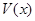取得最大值时，求二面角D－AB－C的余弦值．
粤公网安备 44130202000953号