某企业在第1年初购买一台价值为120万元的设备M，M的价值在使用过程中逐年减少，从第2年到第6年，每年初M的价值比上年初减少10万元；从第7年开始，每年初M的价值为上年初的75%．
（1）求第n年初M的价值
的表达式；
（2）设
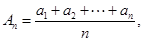若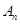
大于80万元，则M继续使用，否则须在第n年初对M更新，
证明：第6年初仍可对M继续使用．
相关试题
的部分图象如图所示.
的解析式；
，求
的值.
的最小值。
恒成立，求实数x的取值范围.
,其中常数a>1.
，在曲线
上的点
处的切线方程是
，且函数在
处有极值。
的解析式
上的最值
，证明
推荐套卷
某企业在第1年初购买一台价值为120万元的设备M，M的价值在使用过程中逐年减少，从第2年到第6年，每年初M的价值比上年初减少10万元；从第7年开始，每年初M的价值为上年初的75%．
（1）求第n年初M的价值的表达式；
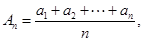（2）设若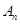大于80万元，则M继续使用，否则须在第n年初对M更新，
证明：第6年初仍可对M继续使用．
粤公网安备 44130202000953号