（本题13分）在几何体ABCDE中，∠BAC=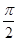 
，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1．
（1）求证：DC∥平面ABE；
（2）求证：AF⊥平面BCDE；
（3）求几何体ABCDE的体积．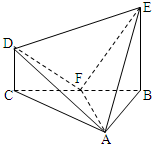
中，
.
的值.
都是锐角，
求
的值.
<4.
中，
求
与
，且
满足
，求
的最小值.推荐套卷
（本题13分）在几何体ABCDE中，∠BAC= 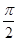，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1．
（1）求证：DC∥平面ABE；
（2）求证：AF⊥平面BCDE；
（3）求几何体ABCDE的体积．
粤公网安备 44130202000953号