如图,在Rt△ABC中,AB=AC,∠BAC=90,O为BC的中点。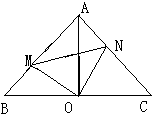
(1)写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,请证明你的结论。
相关知识点
推荐套卷
如图,在Rt△ABC中,AB=AC,∠BAC=90,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,请证明你的结论。