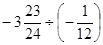计算下列各题（每题4分，共32分）
⑴-20+（-14）-（-18）-13 ⑵ 10+（-2）×（-5）2
（3）
÷
-
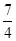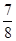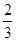×（-6） （4）（-
-
+
）÷（-
）
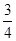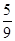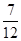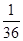（5）∣-
∣÷（-
）-
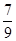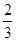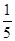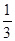×（-4）2 （6）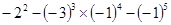
（7）
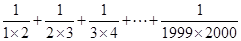(8) 
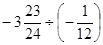
相关知识点
推荐套卷
计算下列各题（每题4分，共32分）
⑴-20+（-14）-（-18）-13 ⑵ 10+（-2）×（-5）2
（3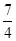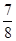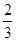）÷-×（-6） （4）（--+）÷（-）
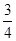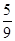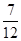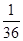（5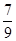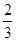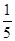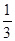）∣-∣÷（-）-×（-4）2 （6）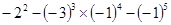
（7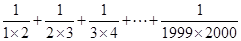） (8)
粤公网安备 44130202000953号